About the model
The value of information application provides an understanding of how much health is potentially gained with every incremental increase in sample size, and can calculate the optimal sample size (one that maximizes health) for your study given your budget.
What’s “beneath the hood?”
The underlying premise of VOI is that a decision to select one strategy over an alternative based on current information is with some probability the wrong choice, the consequence thereby resulting in an opportunity cost. For example, patients in Intervention A compared to Usual Care experience a relative improvement in achieving alcohol abstinence by a relative risk = 1.5 and a comparatively higher expected net benefit (health gain). Based on the current information a decision maker would choose intervention A over Usual Care as it maximizes health. However, the accuracy over the relative effect of the intervention is uncertain thereby raising the possibility that the decision to always choose Intervention A is incorrect. Considering that the true effect of the intervention falls within a range, with Intervention A yielding a greater net benefit over Usual Care 60% of the time, the decision maker makes an incorrect choice 40% of the time and an opportunity cost is incurred. Thus a rationale for collecting new information (by conducting research) is established in order to improve decision making. The total opportunity cost is the maximum society should pay for additional research and reflects the value of information.
The two VOI metrics currently available on TORCH are expected value of sample information (EVSI) and expected net benefit of sampling (ENBS). Both are useful to identify an optimal sample size of a study (i.e., one that maximizes health) when there are no budget constraints as well as when one is imposed, and for understanding the expected net benefit (health gains) of incremental increases in sample size. Across a range of sample sizes, EVSI compares the expected net benefit of a decision made with current information and the expected net benefit of a decision made if current information were updated with additional more precise information.
Formally, 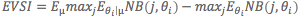 where the first half of the equation is a Bayesian calculation of the posterior expected net benefit of the selected strategy after intervention effect sizes have been updated with “new” information and the second half is the expected net benefit of a decision made with current information. Of course, the new information does not come from an actual study and no real data has been collected, instead estimates are simulated based on prior knowledge of the effect size, variance, distribution, and sample size. The use of simulated data is actually preferred for updating posterior information to avoid introducing potential biases that data from a real world study may bring (i.e., the difference in net benefit, EVSI, may be attributable to differences in study design and population).
where the first half of the equation is a Bayesian calculation of the posterior expected net benefit of the selected strategy after intervention effect sizes have been updated with “new” information and the second half is the expected net benefit of a decision made with current information. Of course, the new information does not come from an actual study and no real data has been collected, instead estimates are simulated based on prior knowledge of the effect size, variance, distribution, and sample size. The use of simulated data is actually preferred for updating posterior information to avoid introducing potential biases that data from a real world study may bring (i.e., the difference in net benefit, EVSI, may be attributable to differences in study design and population).
For the TORCH VOI calculations, the uncertainty over the relative effect of an intervention is propagated through the HIV transmission or progression models which are used to generate QALYs (effectiveness) and intervention costs for every possible effect size and range of sample sizes. See Ades and Briggs for a detailed description. The intervention effect, its impact on downstream parameters, and uncertainty were established based on a systematic literature review and inputs were chosen based on a hierarchy of evidence where priority was given to meta-analysis followed by randomized control trials then non-randomized studies. Individual EVSI is then calculated for a matrix of willingness to pay thresholds and sample sizes. As the intervention can benefit more than just an individual, a population EVSI is calculated for current and incident patients (target population) over the intervention’s effective lifetime (duration of intervention effect). Finally, to identify the optimal sample size the expected net benefit of sampling (ENBS) is calculated by subtracting from EVSI the cost of the study. The peak of the ENBS curve is the optimal sample size as it is where the greatest health is expected after subtracting out the cost of the study.
While the use of a VOI framework for decision making has gained increasing interest in health care it has yet to gain widespread use as it generally requires a sufficiently complex mathematical model that propagates the uncertainty of real world phenomena and can be conceptually and computationally overwhelming. We have removed these obstacles by writing a program to calculate the VOI metrics using simulated data generated by a robust HIV transmission and progression model developed by a team of researchers in the Division of Comparative Effectiveness and Decision Science at New York University School of Medicine.
Resources:
Ades AE, Lu G, Claxton K. Expected value of sample information calculations in medical decision modeling. Medical decision making : an international journal of the Society for Medical Decision Making. Mar-Apr 2004;24(2):207-227. http://www.ncbi.nlm.nih.gov/pubmed/15090106Briggs A, Claxton K, Sculpher M. Decision Modeling for Health Economic Evaluation. New York: Oxford University Press; 2006.
Claxton K, Neumann PJ, Araki S, Weinstein MC. Bayesian value-of-information analysis. An application to a policy model of Alzheimer's disease. International journal of technology assessment in health care. Winter 2001;17(1):38-55. http://www.ncbi.nlm.nih.gov/pubmed/11329844
Claxton K, Sculpher M, Drummond M. A rational framework for decision making by the National Institute For Clinical Excellence (NICE). Lancet. Aug 31 2002;360(9334):711-715.
How Does Value of Information Differ from a Power Analysis?
Statistical power analysis is often used to determine the minimum sample size required to detect a desired effect size for a given risk of a Type I error (accepting the alternative hypothesis when in fact the null is true, “false positive”). The concern with this method is sampling enough participants (or clusters) to adequately power the type of analysis the investigator wishes to conduct in order to detect an intervention’s “true” effect. As accepted as this method is by the research community, its usefulness is limited considering that the calculations ignore the study budget explicitly and does not relate incremental increases in sample size to potential gains in health or return on investment, which after all is the main purpose of most health studies. A value of information framework, particularly the metrics “expected value of sample information” and “expected net benefit of sampling,” explicitly ties incremental sample size increases to health and can answer the questions:
- 1) For my budget, what is the optimal sample size for my study? i.e., How much more health can I gain for every incremental increase in sample size?
- 2) At what sample size will I no longer realize a return (health benefit) on my investment and should stop acquiring additional participants?
- 3) Given my willingness to pay for 1 additional quality adjusted life year, is conducting my study worthwhile? i.e., will the information I produce impact the current decision being made and be useful to decision makers?
In summary, value of information provides an understanding of how much health is potentially gained with every incremental increase in sample size, and can calculate the optimal sample size (one that maximizes health) for your study given your budget.
See a worked out example of the VOI East Africa Sample Size CalculatorResources:
Ades AE, Lu G, Claxton K. Expected value of sample information calculations in medical decision modeling. Medical decision making : an international journal of the Society for Medical Decision Making. Mar-Apr 2004;24(2):207-227. http://www.ncbi.nlm.nih.gov/pubmed/15090106Example: What is the optimal sample size for my study which tests an intervention aimed at reducing alcohol consumption among HIV+ patients on antiretroviral therapy?
Coming soon…
How to cite the sample size calculator
Coming soon…